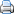50 verspillingen op kantoor volgens Lean Office Innovation
Gepubliceerd in
Lean Six Sigma
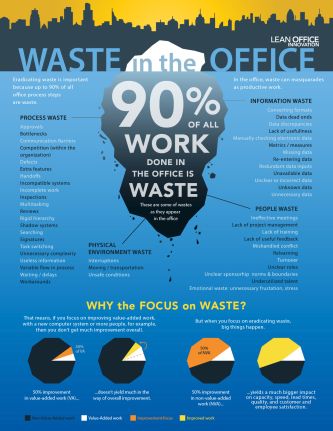
Volgens Lean Office Innovation zijn er 50 mogelijke verspillingen in een kantooromgeving. Ze organiseerden een ontwerpwedstrijd om van deze verspillingen een leuke infographic te maken. Bekijk hier alle inzendingen. Mocht je niet visueel zijn ingesteld, dan volgt hieronder de tekstuele variant:
Process Waste
- Approvals
- Bottlenecks
- Communication barriers
- Competition (within the organization)
- Defects
- Extra features
- Handoffs
- Incompatible systems
- Incomplete work
- Inspections
- Multitasking
- Reviews
- Rigid hierarchy
- Shadow systems
- Searching
- Signatures
- Task switching
- Unnecessary complexity
- Useless information
- Variable flow in a process
- Waiting/delays
- Workarounds
Physical Environment Waste
- Interruptions
- Moving/transportation
- Unsafe conditions
Information Waste
- Converting formats
- Data dead ends
- Data discrepancies
- Lack of usefulness
- Manually checking electronic data
- Metrics/measures
- Missing Data
- Re-entering data
- Redundant data inputs
- Redundant data inputs
- Unavailable data
- Unclear or incorrect data
- Unknown data
- Unnecessary data
People Waste
- Ineffective meetings
- Lack of project management
- Lack of training
- Lack of useful feedback
- Mishandled conflict
- Relearning
- Turnover
- Unclear roles
- Unclear sponsorship, norms, & boundaries
- Underutilized talent
- Emotional waste: unnecessary frustration, stress
Laatst aangepast op donderdag, 04 januari 2018 05:47
LSS: Boxplot (Box-and-Whisker plot)
Gepubliceerd in
Lean Six Sigma
De kenmerken van een verdeling worden vaak samengevat door middel van het zogenaamde vijf-getallenresumé. Het vijf-getallenresumé wordt gevormd door respectievelijk:
-
De laagste uitslag in de gegevens.
-
Het eerste kwartiel (Q1, 25ste percentiel: een kwart van de waarnemingen ligt beneden deze score).
-
De mediaan, waarbeneden de helft van de waarnemingen valt.
-
Het derde kwartiel (Q3, 75ste percentiel).
-
De hoogste uitslag.
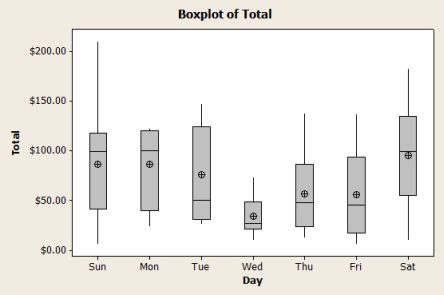
Het vijf-getallenresumé kan grafisch worden weergegeven in een boxdiagram (box plot). De Engelse benaming hiervoor is box-and-wisker plot, letterlijk doos-met-snorharen plaatje.
In een boxplot geldt:
-
De onder- en bovenkant van de box liggen bij de kwartielen, zodat de lengte van de box gelijk is aan de interkwartielafstand. De box bevat dus de helft van alle waarnemingen; de breedte van de box zegt niets; die is altijd hetzelfde.
-
De mediaan wordt in de box aangegeven door en streep.
-
De lijnenboven en onder de box (de 'snorharen') lopen tot de grootste en kleinste waarneming. Beneden de onderrand van de box bevindt zich dus het kwart van de gevallen met de laagste waarden; boven de bovenrand het kwart met de hoogste waarden.
Het centrum, de spreiding en het totale bereik van de verdeling zijn uit de boxplot direct te herkennen. Als de mediaan in het midden van de box ligt en als de snorharen niet even lang zijn, duidt dit op een scheve verdeling.
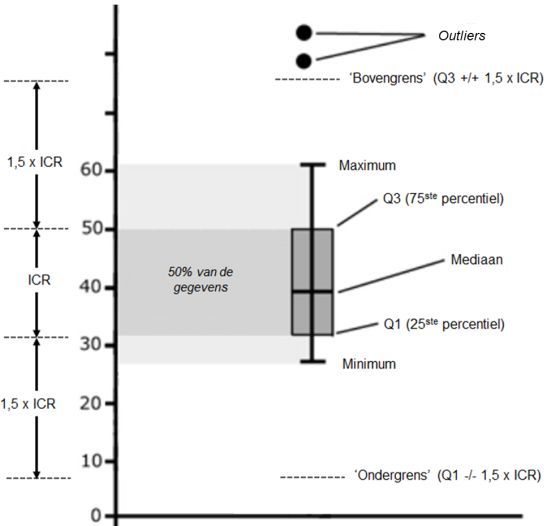
Bron: Statistiek in woorden, Anke Slotboom
Laatst aangepast op vrijdag, 30 maart 2018 05:55
LSS: Individual Value Plot (IVP)
Gepubliceerd in
Lean Six Sigma
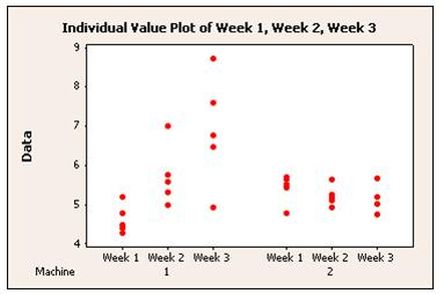
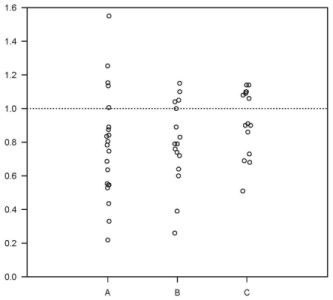
Een Individual Value Plot (IVP) is een grafiek waarmee je individuele datapunten kunt beoordelen. De IVP geeft elk datapunt weer voor elke groep (in dit geval de weken), zodat je snel en makkelijk uitschieters kunt zien en een beeld krijgt van de spreiding.
De IVP geeft dezelfde gegevens weer als de Box plot. Bij kleinere subgroepen, geeft de IVP meer 'gevoel' bij de verdeling van de data. Als er veel datapunten zijn binnen een subgroep, zullen de punten al snel een verticale lijn vormen. Binnen Minitab is het mogelijk de datapunten te verspreiden over een bepaalde bandbreedte, zodat ze niet overlappen. Dit wordt 'wiebelen' (Jitter) genoemd. Omdat hierbij de datapunten random worden gespreid, betekent dit wel dat elke IVP uniek is.
Laatst aangepast op zondag, 31 december 2017 07:52
LSS: centrale limietstelling
Gepubliceerd in
Lean Six Sigma
Het begrip steekproefverdeling (Engels: sampling distribution) speelt een centrale rol in dát deel van de statistiek waar we op basis van een onderzoek van een steekproef uitspraken willen doen over een groter geheel, de populatie (inferentiële statistiek). Het probleem is dat een steekproef altijd maar één willekeurige greep is uit de populatie. Als je een andere, even representatieve steekproef onderzoeken, dan is het zeer aannemelijk dat deze een net iets ander beeld te zien geeft.
Als je steeds opnieuw steekproeven zou trekken en steeds het gemiddelde van elke steekproef zou berekenen, zou je een frequentieverdeling van de gevonden gemiddelden kunnen tekenen. Op de horizontale as zet je dan alle gevonden waarden uit en verticaal geef je aan hoe vaak een bepaald gemiddelde is gevonden. Je kunt hier onbeperkt mee doorgaan, maar uiteindelijk zullen de meeste gevonden steekproefgemiddelden in de buurt van het populatiegemiddelde liggen. Door toevalligheden in de steekproef trekking zullen er ook 'afwijkende' waarden gevonden worden. Naarmate de afwijking van het populatiegemiddelde groter is, wordt de kans dat men zo'n steekproefgemiddelde vindt echter steeds kleiner.
Zelfs zonder één steekproef te trekken is puur theoretisch de precieze vorm van de frequentieverdeling van steekproefgemiddelden af te leiden, weergegeven als een kansverdeling. Deze kansverdeling wordt de steekproefverdeling (van het gemiddelde) genoemd. Een steekproefverdeling van het gemiddelde is een theoretische kansverdeling van de mogelijke waarden van het gemiddelde als je een oneindig aantal steekproeven van een gegeven grootte zou bekijken. Naast een steekproefverdeling voor het gemiddelde kun je voor elke statistiek een steekproefverdeling maken (mediaan, variantie, etc.).
De standaardafwijking van een steekproef verdeling wordt de standaardfout genoemd. De standaardafwijking van een steekproefverdeling van het gemiddelde heet de standaardfout van het gemiddelde. Hoe groter de standaardfout, des te meer zullen dus de gemiddelden van steekproef tot steekproef kunnen variëren.
De standaardfout hangt behalve van de steekproefgrootte, ook af van de spreiding van de eigenschap in de populatie. Een grote standaardfout betekent dat het berekende steekproefgemiddelde geen goede schatter is voor het populatiegemiddelde.
In dit verband is de centrale limietstelling volgens Slotboom een uiterst een uiterst nuttige stelling:
- Naarmate de steekproefomvang groter is, zal de steekproefverdeling van het gemiddelde meer lijken op een normale verdeling. Dit geldt ongeacht de vorm van de populatieverdeling.
- Het gemiddelde van de steekproefverdeling van het gemiddelde, zal gelijk zijn aan de waarde van het populatiegemiddelde
- De standaardfout van het gemiddelde is te berekenen uit de spreiding van de eigenschap in de populatie en de steekproefgrootte (probleem hierbij is wel dat de spreiding - variantie - in de populatie meestal onbekend is).
Ingewikkelde materie! In het filmpje Bunnie, Dragons and the 'Normal' World een Jip-en-Janneke-uitleg van de centrale limietstelling.
Bron: Statistiek in woorden, A. Slotboom
Laatst aangepast op donderdag, 21 december 2017 20:42
KR8 volgens Rijkswaterstaat
Gepubliceerd in
Lean Six Sigma

Rijkswaterstaat (RWS) heeft haar Lean Six Sigma-programma 'KR8' genoemd.
KR8 staat voor:
-
Klantwaarde voorop
-
Respect voor mensen
-
8 verspillingen
Het onderstaande citaat ondersteunt de filosofie achter KR8:

Lean Six Sigma is geen methodiek die je vrijblijvend toepast, maar een compleet andere opvatting van werken en handelen. Onderdeel van die transformatie, kaikaku in het Japans, is het herontwerpen van je organisatie. Dat kan alleen door samen vast te stellen wat nu echt waarde aan je product of dienst toevoegt en wat verspillingen zijn. Daarom kiest Rijkswaterstaat met KR8 nadrukkelijk voor verandering vanaf de werkvloer. Jezelf permanent blijven ontwikkelen en verbeteren, daar gaat het uiteindelijk om.
Bron: Klantwaarde als eindproduct, Rijksoverheid omarmt management-filosofie Lean Six Sigma, Eric Weijers
Laatst aangepast op maandag, 01 januari 2018 13:07
LSS: Spaghettidiagram
Gepubliceerd in
Lean Six Sigma
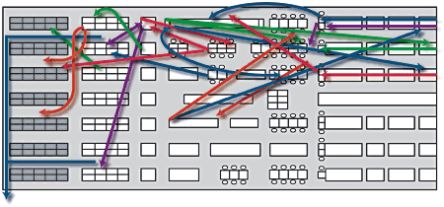
Een spaghettidiagram - ook wel loopschema's genoemd - is een grafische weergave van de verplaatsing van materiaal of mensen binnen een proces. Het diagram toont als het ware de verspilling 'in actie' en is dan ook een bruikbaar hulpmiddel voor het analyseren van verkeer of beweging.
Met een spaghettidiagram visualiseer je de route die een 'product' aflegt door de organisatie (Womb-to-Tomb) of de route die een werknemer aflegt om de taak te voltooien. Op deze manier blijkt vaak dat de route onnodig lang is en krijg je aanknopingspunten voor het verbeteren van de indeling van de werkruimte(s).
Laatst aangepast op zondag, 31 december 2017 07:52
LSS: Bluff Your Way Into steekproeven
Gepubliceerd in
Lean Six Sigma
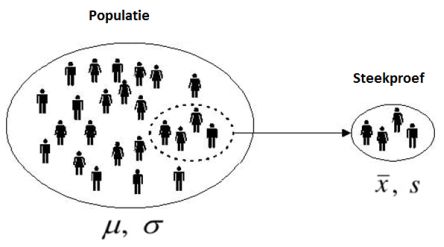
Binnen de (inferentiële) statistiek probeer je vaak op grond van de resultaten van een steekproef conclusies te trekken over de populatie. De populatie is de naam voor de complete groep waarover het statistisch onderzoek gaat. De steekproef is het deel van de populatie dat je bij je onderzoek betrekt. Er zijn twee redenen waarom je gebruik maakt van een steekproef. De eerste is dat de populatie zo groot is dat het onmogelijk is om alle objecten te benaderen. De tweede reden is dat het onderzoek te duur wordt om bij alle objecten metingen te verrichten. Door de inferentiële statistiek toe te passen, is het ook niet noodzakelijk om een hele populatie te bemeten. Ook door slechts een deel van de populatie te bemeten, is de onderzoeker in staat om relevante uitspraken te doen over die populatie.
Bij statistisch onderzoek moet je steeds goed onderscheiden of je over de populatie spreekt dan wel over de steekproef. De populatie is over het algemeen slechts in formele zin gegeven in termen van een kansverdeling met enkele onbekende parameters. Het zijn deze parameters die men graag zou kennen, maar om uiteenlopende redenen niet kent. Een steekproef verschaft informatie over de parameters, door het geven van een schatting, het toetsen van een hypothese over een parameter, e.d. Zo is er het populatiegemiddelde, meestal onbekend, en als schatting daarvan het steekproefgemiddelde. Evenzo is de steekproefvariantie een schatting van de populatievariantie, enzovoorts.
Bij het doen van onderzoek is het - zoals gezegd - zelden mogelijk om alle elementen waarin men geïnteresseerd is (de populatie) te onderzoeken. Je onderzoekt dan een steekproef van elementen uit die populatie. Wil je met enig vertrouwen op basis van een steekproef uitspraken doen over een populatie, dan moet de steekproef representatief en willekeurig (aselect) getrokken zijn. Bij een aselecte steekproef heeft ieder element van de populatie een even grote kans om in de steekproef opgenomen te worden. Uitspraken over populaties zijn altijd kansuitspraken; je weet het nooit helemaal zeker, juist omdat je niet de hele populatie, maar slechts een steekproef onderzocht hebt.
De onafhankelijkheid van steekproeven houdt in dat het trekken van een steekproefelement in de ene steekproef geen invloed heeft op het trekken van elementen in andere steekproeven. De scores in de verschillende steekproeven zijn dan ook onderling onafhankelijk, met andere woorden, alle individuen of observaties in alle steekproeven zijn toevalsgewijs.
In een onderzoek waarin bijvoorbeeld twee groepen van respondenten met elkaar worden vergeleken, en in de éne steekproef enkel mannen zitten, en in de andere enkel de partners van diezelfde mannen, spreek je van afhankelijke of gerelateerde steekproeven. Andere voorbeelden van gerelateerde steekproeven zijn: het afnemen van een vragenlijst bij een aantal personen en het na verloop van een maand afnemen van dezelfde vragenlijst bij dezelfde personen, of het indelen van studenten in twee groepen: een testgroep en een controlegroep. De studenten worden niet toevalsgewijs verdeeld over de test- of controlegroep maar telkens als een student toegewezen wordt aan de testgroep, wordt een andere student met zoveel mogelijk dezelfde karakteristieken als eerste toegewezen aan de controlegroep (dit is een gepaarde steekproef). Gepaarde waarnemingen zijn meetresultaten bij dezelfde onderzoekseenheid.
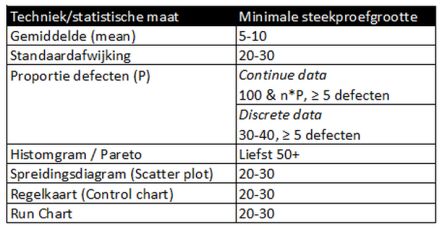
Aan een steekproef wordt niet alleen de eis gesteld van representativiteit (= respons is representatief voor de populatie waarover de onderzoeker een uitspraak wil doen), maar gelden ook eisen ten aanzien van de omvang van de steekproef. De steekproef moet voldoende groot zijn om statistisch relevante verbanden en verschillen te vinden maar ook niet te klein om onnodig geld te verspillen.
Aan deze eis kan worden voldaan door vooraf de minimale steekproefomvang te bepalen.
De sterkte van een steekproef (power) wordt getalsmatig beïnvloed door het aantal steekproeven, de waargenomen variatie en het verschil dat waargenomen moet kunnen worden.
Bepalen van de omvang van een steekproef
Voor het bepalen van de steekproefomvang kan gebruik gemaakt worden van de zogenaamde betrouwbaarheidsintervalmethode (confidence interval approach). De methode van het betrouwbaarheidsinterval is een methode, waarbij de begrippen: nauwkeurigheid (steekproeffout), variabiliteit (variability) en het betrouwbaarheidsinterval (confidence interval) worden gecombineerd om een ‘juiste’ steekproefomvang te nemen.
Binnen betrouwbaarheidsintervalmethode staan - zoals gezegd - drie begrippen centraal:
-
Nauwkeurigheid (steekproeffout): het verschil tussen de steekproefuitkomst en de werkelijke populatiewaarde vanwege het feit dat er een steekproef is getrokken.
-
Variabiliteit (variability): Variabiliteit: omschreven als de mate van verschil (of overeenkomst) in de antwoorden van de respondenten op een bepaalde vraag. De variabiliteit wordt berekend door het vermenigvuldigen van p en q, waarbij p staat voor het geschatte percentage in de populatie en q voor het resterende deel van de populatie (100 - p). Hoe groter de variabiliteit, hoe groter de steekproefomvang moet zijn om een bepaalde nauwkeurigheid te bereiken
-
Betrouwbaarheidsinterval (confidence interval): waardegebied waarvan de grenzen een bepaald percentage antwoorden op een vraag omvatten.
Bij het bepalen van de steekproefgrootte wordt uitgegaan van een normale verdeling en de centrale limietstelling.
Bij het bepalen van de steekproefgrootte kun je de normale verdeling gebruiken in verband met de centrale-limietstelling. Ongeacht de vorm van de verdeling van de populatie, zal de verdeling van de steekproeven (als n groter is dan 30) een normale verdeling aannemen. De eigenschappen van de normale verdeling zijn zodanig dat 1,96 maal de standaardafwijking in theorie de grenzen van 95 procent van de verdeling definieert.
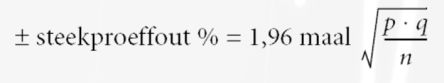
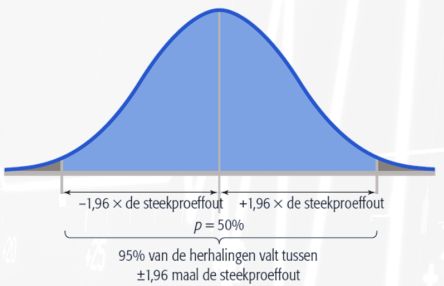
Bij het bepalen van de juiste steekproefomvang, hoef je slechts drie factoren in overweging te nemen:
-
De (verwachte) mate van variabiliteit in de populatie; bij het bepalen van de variabiliteit in de populatie, geldt als praktische overweging dat je bij het bepalen van de steekproefomvang uitgaat van het slechtste geval(p=50, q=50).
-
De gewenste nauwkeurigheid; bij het vaststellen niveau van de gewenste steekproeffout, geldt dat meestal gegeven is wat een acceptabele steekproeffout is. Vaak is dit +/- 5%. De hoogte van de steekproeffout zal - vanzelfsprekend - afhangen van het belang van de beslissing die op basis van de steekproefresultaten genomen moet worden.
-
Het vereiste betrouwbaarheidsniveau van je schattingen van de populatiewaarden; bij het vaststellen van het gewenste betrouwbaarheidsniveau geldt dat hoe hoger het betrouwbaarheidsniveau moet zijn, des te groter de steekproefomvang wordt. Gebruikelijk is om hiervoor 95% te nemen (z=1,96). Bij een betrouwbaarheidsniveau van 99% hoort een z-waarde van 2,58.
Als het bovenstaande is gespecificeerd, kan op basis van de onderstaande formule de steekproefomvang worden berekend:

Bron: Principes van marktonderzoek, Alvin C. Burns, Ronald F. Bush, Ingrid Smeets
Laatst aangepast op vrijdag, 22 december 2017 21:01
Kwaliteit volgens Donald J. Wheeler
Gepubliceerd in
Lean Six Sigma
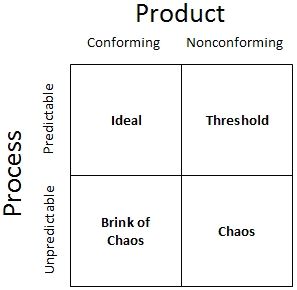
Volgens Donald J. Wheeler is het bij kwaliteitszorg (quality control) nodig om duidelijk onderscheid te maken tussen het proces en het product. Producten kunnen worden gekarakteriseerd door het al dan niet voldoen aan de klanteisen (conformance to specifications). Processen kunnen worden gekenmerkt door hun voorspelbaarheid. Als je beide aspecten combineert krijg je een matrix met vier mogelijke toestanden waarin een proces zich kan bevinden:
-
De ideale staat (ideal state): het proces wordt statistisch gecontroleerd en voldoet aan de vereisten van de klant.
-
Drempelgeval (treshold): proces is statistisch onder controle, maar voldoet niet aan de eisen van de klant.
-
Rand van de afgrond (brink of chaos): proces voldoet aan vereisten van de klant, maar is statistisch nog niet onder controle. Het proces bevat speciale oorzaken (special cause variation) en is onvoorspelbaar.
-
Chaos: proces is statisch niet onder controle en voldoet niet aan de eisen van de klant. Het is belangrijk eerst de speciale oorzaken uit het proces te verwijderen voordat je andere procesverbeteringen doorvoert. Anders zullen ze de verbeterinspanningen tegenwerken.
Bron: The Four Possibilities for Any Process, Donald J. Wheeler
Laatst aangepast op vrijdag, 13 april 2018 06:40
LSS: Run chart
Gepubliceerd in
Lean Six Sigma
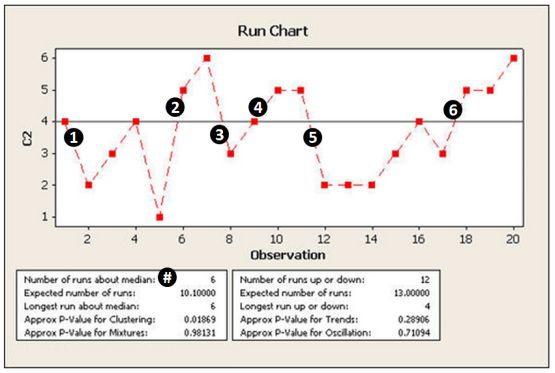
Een grafiek van gegevens in de volgorde waarin ze zich voordoen waarbij de mediaan centraal staat. Een run chart is een hulpmiddel om te beoordelen of een proces stabiel is.
Een Run Chart is een hulpmiddel om procesprestaties te analyseren op trends, verschuivingen (shifts) en/of patronen. Je zoekt signalen dat speciale factoren van invloed zijn op de variabiliteit van een proces. Zoals bijvoorbeeld ongewoon lange runs van de datapunten boven of onder de mediaan-/gemiddelde-lijn, het totale aantal van dergelijke runs in de data set, en de ongewoon lange reeks van opeenvolgende stijgingen of dalingen. Vaak is verder onderzoek nodig om uitzoeken wat er precies aan de hand is.
Een Times Series Plot (tijddiagram) is niet altijd voldoende om te beoordelen of het proces stabiel is. Soms zie je te veel (trends die er eigenlijk niet zijn) en soms zie je te weinig. De run chart is een hulpmiddel om snel en gemakkelijk te zien of het proces (statistisch) stabiel is.
Binnen een Run Chart kun je op twee manieren zoeken naar zogenaamde 'runs'.
-
Het aantal runs boven en onder de mediaan (of het gemiddelde). Dit wordt 'Runs about the median' (of 'Runs about the mean') genoemd: één enkele 'run about the median' is een aantal elkaar in tijd opvolgende datapunten die allemaal aan één kan van de mediaanlijn vallen. De run stopt zodra de mediaan-lijn wordt doorkruist (op de lijn telt dus nog mee!).
-
Het aantal opgaande en neergaande runs, de zgn. 'Runs up or down': een run naar boven of beneden is het aantal elkaar in tijd opvolgende datapunten die allemaal stijgen respectievelijk dalen. De run stop zodra de richting van de lijn stopt.
Om een run chart te kunnen maken heb je minimaal 20 datapunten nodig.
Het onderstaande scherm laat zien hoe je in Minitab een Run Chart kunt maken (via optie Stat/Quality Tools/Run Chart). Er zijn 2 spannende keuzes te maken. Allereerst moet je aangeven uit hoeveel kolommen je dataset bestaat. Als er meerdere groepen data zijn (bijvoorbeeld bij meerdere groepen van metingen op hetzelfde moment). De andere keuze is of je als het gaat om de centrummaat gebruik wilt maken van de mediaan ('Plot subgroup(s) medians') of het gemiddelde ('Plot subgroup(s) means'). Door gebruik te maken van de mediaan elimineer je de impact van uitschieters in de dataset. Als je geen uitschieters hebt, is het gemiddelde ook prima bruikbaar.
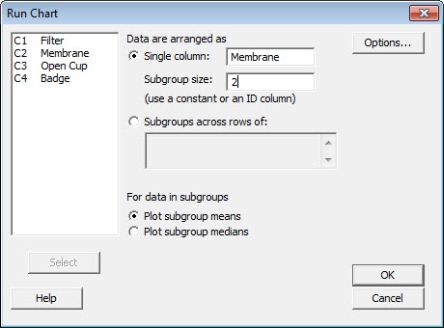
Laatst aangepast op zondag, 31 december 2017 07:52
LSS: Change Acceleration Process (CAP) volgens G.E.
Gepubliceerd in
Lean Six Sigma
Change Acceleration Process (CAP) is een binnen GE ontwikkelde aanpak voor verandermanagement. Binnen General Electric (GE) was Jack Welch op zoek naar de best practice op het gebied van verandermanagement met als doel deze te vertalen naar een praktische aanpak die bruikbaar was voor alle GE-managers. Dit resulteerde in 1992 in het Change Acceleration Process (CAP).
CAP is dus het resultaat van een grondig onderzoek naar de succesfactoren bij veranderingsprojecten en vormt een stappenplan voor het snel implementeren van veranderinitiatieven. De aanpak is gebaseerd op de aanname dat succesvolle verandering afhangt van twee factoren:
-
De (inhoudelijke) kwaliteit van de verandering [Q].
-
De organisatorische, culturele, politieke en personele aspecten van de verandering, oftwel de acceptatie - de buy-in en commitment - van de verandering [A].
De effectiviteit van de verandering (E) kan worden gedefinieerd als het resultaat van beide aspecten.

De kwaliteit van de 'Q' is bijna nooit de oorzaak van het mislukken van de verandering. De meeste veranderinitiatieven falen vanwege het verwaarlozen van organisatorische, cultulere en politieke aspecten van de verandering, oftewel de 'A' van de verandering. Anders gezegd: de meeste organisatie besteden niet genoeg tijd aan de mensenlijke component van de verandering.
CAP richt zich juist wel op de acceptatie van de verandering; bij CAP is de 'buy-in' ingebouwd in de aanpak. CAP begint met een vaak vergeten waarheid van verandering: 'A champion needs to sponsor and lead the change'. Het succes van een veranderpoging is bijna altijd recht evenredig met de vaardigheden van haar 'champion'.
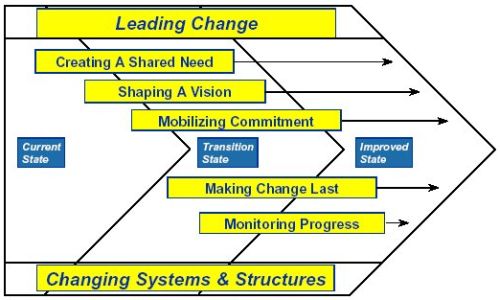
Het CAP-model is een 'veranderingsmodel' dat vaak gebruikt wordt in combinatie met Lean Six Sigma. Het model bestaat uit stappen voor het snel, succesvol invoeren van verandering:
-
Leading change: leiderschap zodanig activeren dat het de motor wordt achter het veranderingsproces.
-
Creating a shared need: bewerkstelligen van een gedeeld besef van urgentie van verandering bij alle betrokkenen.
-
Shaping a vision: vormgeven van een beeld van het gewenste resultaat van het veranderingstraject.
-
Mobilizing commitment: mobiliseren van betrokkenheid bij iedereen die voor het behalen van het succes cruciaal is.
-
Making change last: verankeren van veranderingsprocessen in de organisatie.
-
Monitoren progress: realiseren van verbeteringen en de vooruitgang monitoren door te blijven meten en de meetprocessen te formaliseren.
-
Changing systems and structures: installeren van de nieuwe organiatie-elementen, zoals processen, rollen en verantwoordelijkheden.
Bron: Leidinggeven aan Six Sigma - Praktijklessen voor managers en projectleiders, Rini van Solingen, e.a.
Laatst aangepast op vrijdag, 22 december 2017 20:58
|



 Lean Six Sigma
Lean Six Sigma